Question

Suppose that the future price p(t) of a certain item is given by the following exponential function. In this function, p(t) is measured in dollars and t is the number of years from today. p(t) = 3000 * (1.019) ^ t

Answer 1

Step-by-step explanation

The growth or decay of an original quantity C that increases or decreases in a p% per year after t years is given by the following equation:

`p(t)=C\cdot(1\pm(p)/(100))^t`

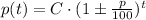
If the quantity increases (i.e. it growths) we use the + symbol inside the parenthesis. If the quantity decreases we use the - symbol. This implies that for a growth the term that is raised to t is greater than 1 and for a decay that term is smaller than 1.

Now let's compare that generic equation with the function given by the question:

`3000\cdot(1.019)^t=C\cdot(1\pm(p)/(100))^t`

One of the first things you can notice is that C=3000 which means that the initial price was $3000. Just to be sure that this is correct we can evaluate p(t) at t=0:

`p(0)=3000\cdot(1.019)^0=3000`

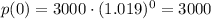
So the initial price was $3000.

Now let's compare the terms inside parenthesis that are raised to t:

`1.019=1\pm(p)/(100)`

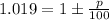
As I stated before, if the term raised to t is greater than 1 then we are talking about a growth. 1.019 is greater than 1 so this function represents a growth. What's more, in the right side of the equation we must use the + symbol. This way we have an equation for the yearly percentage of change of the price:

`1.019=1+(p)/(100)`

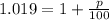
We can substract 1 from both sides of this equation:

`\begin{gathered} 1.019-1=1+(p)/(100)-1 \\ 0.019=(p)/(100) \end{gathered}`

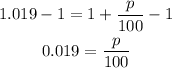
And we multiply both sides by 100:

`\begin{gathered} 100\cdot0.019=(p)/(100)\cdot100 \\ 1.9=p \end{gathered}`

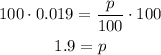
So each year the price increases in a 1.9%.

Answer

Then the answers in order are:

$3000

growth

1.9%