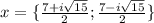Question

I tried it and got imaginary numbers in the answer.

Answer 1

Given the following equation:

`(x)/(x-4)-(4)/(x)=(3)/(x-4)`

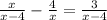
First, we will identify the zeros of the denominator

So, the zeros are: x = {0,4}

Second, multiply the equation by x(x-4) to eliminate the denominators

`x(x-4)*((x)/(x-4)-(4)/(x))=x(x-4)*(3)/(x-4)`

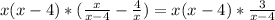
Simplify the equation:

`x^2-4(x-4)=3x`

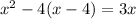
Expand the equation and combine the like terms:

`\begin{gathered} x^2-4x+16=3x \\ x^2-7x+16=0 \end{gathered}`

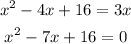
The last quadratic equation will be solved using the quadratic rule:

`x=(-b\pm√(b^2-4ac))/(2a)`

Substitute a = 1, b = -7, c = 16

`\begin{gathered} x=(7\pm√((-7)^2-4(1)(16)))/(2(1)) \\ \\ x=(7\pm√(-15))/(2)=(7\pm i√(15))/(2) \\ \\ x=\lbrace(7+i√(15))/(2);(7-i√(15))/(2)\rbrace \end{gathered}`

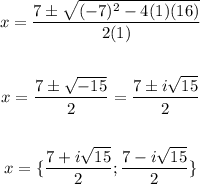
So, the answer will be:

`x=\lbrace(7+i√(15))/(2);(7-i√(15))/(2)\rbrace`