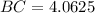We are given two similar triangles which are;
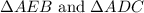
Note that the sides are not equal, but similar in the sense that the ratio of two sides in one triangle is equal to that of the two corresponding sides in the other triangle.
To calculate the length of side BC, we can use any of the following ratios (proportions);

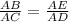
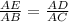
Using the first ratio as stated above, we shall have;
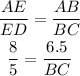
Next we cross multiply and we have;
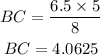
ANSWER: