According to the theorem, the corresponding angles, formed by a transversal on a pair of parallel sides, are always equal.
Also, the sum of angles on a straight line is 180 degree.
The angles 5 and 7 constitute a pair of corresponding angles, formed by the transversal 'r' on the pair of parallel sides 'p' and 'q'. So they must be equal,
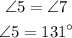
The angles 4 and 5 constitute a straight line, so they must add up to be 180 degrees,
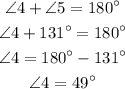
Thus, the angle 4 measures 49 degrees.