Question

Assume a water strider has a roughly circular foot of radius 0.0203 mm. The surface tension of water is 0.0700 N/m.A. What is the maximum possible upward force on the foot due to surface tension of the water? NB. What is the maximum mass of this water strider so that it can keep from breaking through the water surface? The strider has six legs. mg

Answer 1

Part (A)

The maximum possible upward force acting on the foot is,

`F=2\pi r\sigma`

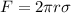
Substitute the known values,

`\begin{gathered} F=2(3.14)(0.0203\text{ mm)(}\frac{10^(-3)\text{ m}}{1\text{ mm}})(0.0700\text{ N/m)} \\ =8.9*10^(-6)\text{ N} \end{gathered}`

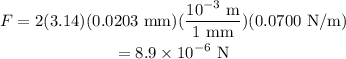
Thus, the maximum possible upward force on the foot is

`8.9*10^(-6)\text{ N}`

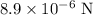
Part (B)

The maximum force due to six legs can be expressed as,

`6F=mg`

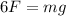
Substitute the known values,

`\begin{gathered} 6(8.9*10^(-6)N)=m(9.8m/s^2) \\ m=\frac{6(8.9*10^(-6)\text{ N)}}{9.8m/s^2}(\frac{1kgm/s^2}{1\text{ N}}) \\ =(5.45*10^(-6)\text{ kg)(}\frac{1\text{ mg}}{10^(-6)\text{ kg}}) \\ =5.45\text{ mg} \end{gathered}`

Thus, the maximum mass of water strider is 5.45 mg.