For this problem, we need to describe a real-life situation where trigonometric functions can be used to model the problem.
Let's assume that a certain vehicle's position is controlled by the speeds of the wheels on each side of the car. Whenever the speeds on the left wheels and right wheels are equal, then the car moves forward, if the speed on the left side is greater than the one on the right side the car goes right, and if the speed on the right side is greater, then the vehicle goes to the left side. This type of car is called a differential drive car, and it's very common on remote-controlled (RC) vehicles.
If we want to model the speed of the car in a two dimensional grid, such as below:
We need to assume that the vehicle will have two components of velocity, one that is parallel to the x-axis and one that is parallel to the y-axis. These will form the linear velocity for the vehicle. We also need an angular velocity, which is the rate at which the angle of the vehicle changes.
If we assume that the wheels of the vehicles are at a distance of "L" apart from each other, then we can model the angular velocity of the vehicle as:
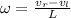
Where "vr" is the speed on the right wheel, and "vl" is the speed on the left wheel. The movement will happen with the center of the car as the center of the movement, with this we can assume that the velocity of the vehicle on the two axes should be:
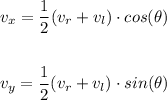
Therefore we can describe the vehicle speed with the following equations:
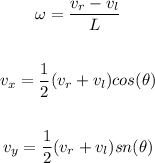
The input variables are "vr" and "vl" which are the speeds of each wheel and the angle of the vehicle "theta", the output is the speed at the x coordinate and the speed at the y coordinate, and the angular speed.
This works very well because if the vehicle is moving parallel to the x-axis, the angle will be 0, the cosine of 0 is 1, therefore the speed on the y axis will be 0 and the speed on the x-axis will be given by 0.5(vr+vl). The opposite happens when the vehicle is moving parallel to the y-axis.