Question

Find the distance between the two points. 15.) (-3, -1), (-1, -5)-use Pythagorean Throrem

Answer 1

4.5 units

Step-by-step explanation:

First, we need to draw the points (-3, -1) and (-1, -5) as follows

Therefore, the distance between the points is the length of the yellow line. This distance is the hypotenuse of a triangle with legs a and b.

The length of a is 2 and the length of b is 4

Then, using the Pythagorean theorem, we can calculate the length of c as follow

`\begin{gathered} c^2=a^2+b^2 \\ c^2=2^2+4^2 \\ c^2=4+16 \\ c^2=20 \end{gathered}`

So, using the calculator, we get that the value of c is equal to

`\begin{gathered} √(c^2)=√(20) \\ c=√(20) \end{gathered}`

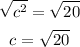
To find an approximate value for c, we will use the following:

We know that √16 = 4 and √25 = 5

Since 20 is between 16 and 25, the square root of 20 is a number between 4 and 5, so we can approximate it to 4.5.

Therefore,

c = 4.5