Question

What is the solution to x^2 – 9x < –8?A. x < 1 or x > 8B. x < –8 or x > 1C. 1 < x < 8D. –8 < x < 1

Answer 1

C. 1 < x < 8

Explanation:

x² - 9x < -8

we will suppose some values for x to check which values will satisfy this inequality:

for x = 1

1(1-9) < -8 which is wrong

for x = 2

2(2-9) < -8 this is satisfying the inequality

for x = 8

8(8-9) < -8 which is wrong

let's take any negative value now,

let x = -2

-2(-2-9) < -8 which is wrong

thus x is the positive value which will always be greater than 1 and less than 8 for the given inequality.

Answer 2

INFORMATION:

We have the next inequality

`x^2-9x<-8`

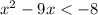
And we must find its solution

STEP BY STEP EXPLANATION:

To solve it, we must:

1. Move all terms aside

`x^2-9x+8<0`

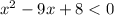
2. Factor x^2-9x+8

`(x-8)(x-1)<0`

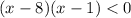
3. Solve for x

`x=8\text{ or }x=1`

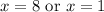
4. From the values of x, we have these 3 intervals to test

`\begin{gathered} x<1 \\ 18 \end{gathered}`

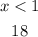
5. Choose a test point for each interval

For the interval x < 1:

`\begin{gathered} \text{ Using x }=0, \\ 0^2-9(0)<-8 \\ 0<-8 \end{gathered}`

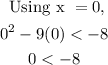
which is false. So, the interval is discarded.

For the interval 1 < x < 8:

`\begin{gathered} \text{ Using x }=2, \\ 2^2-9(2)<-8 \\ -14<-8 \end{gathered}`

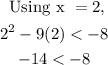
which is true. So, the interval is maintained

For the interval x > 8:

`\begin{gathered} \text{ Using x = 9,} \\ 9^2-9(9)<-8 \\ 0<-8 \end{gathered}`

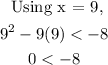
which is false. So, the interval is discarded.

Finally, the solution would be the interval that was maintained: 1 < x < 8.

ANSWER:

C. 1 < x < 8