We are given the following proportions:
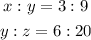
The second proportion is equivalent to:
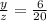
Now, we substitute the value of "z":
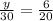
Now, we multiply both sides by 30:
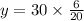
Solving the operation we get:
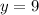
Now, since we have the value of "y" we can use the first proportion to get the value of "x":
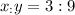
This is equivalent to:
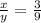
Now, we substitute the value of "y":
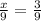
Now, we multiply both sides by 9:
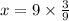
Solving the operations:
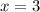
Therefore, the value of "x" is 3.