In this case, we'll have to carry out several steps to find the solution.
Step 01:
Data:
Line A:
point 1 (2,7)
point 2 (-1,10)
Line B:
point 1 (-4,7)
point 2 (-1,6)
Line C:
point 1 (6,5)
point 2 (7,9)
Step 02:
perpendicular lines:
slope of the perpendicular line, m’
m' = - 1 / m
Line A:
slope:
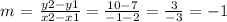
Line B:
slope:
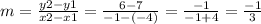
Line C:
slope:
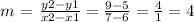
m' = - 1 / m ===> none of the slopes meet the condition
The answer is:
there are no perpendicular lines