Question

Select the correct answer.Consider this equation,tan(6)If 8 is an angle in quadrant II, what is the value of cos(8),OA.B._vOD.

Answer 1

Remember the definition of the tangent function:

`\tan \theta=(\sin \theta)/(\cos \theta)`

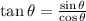
Then, we notice that:

`\tan (\theta)=-\sqrt[]{(19)/(17)=}-\sqrt[]{((19)/(6))/((6)/(17))}=(\sin \theta)/(\cos \theta)`

Then, we can conclude that:

`(\sin \theta)/(\cos \theta)=-\frac{\sqrt[]{(19)/(6)}}{\sqrt[]{(6)/(17)}}`

Something important to remember is that, in quadrant II, the value of sin(x) is positive, whereas the value of cos(x) is negative

So,

`\begin{gathered} \sin (\theta)=\sqrt[]{(19)/(6)} \\ \Rightarrow(1)/(\cos \theta)=-\frac{1}{\sqrt[]{(6)/(17)}} \\ \Rightarrow\cos \theta=-\sqrt[]{(17)/(6)} \end{gathered}`

Therefore, the answer to the question is option A