Given:
• Degree of polynomial = 3
,
• Zeros of the polynomial: 2, 3 - 2i
Let's find the polynomial.
Since the polynomail is of degree 3, it's highest exponent will be 3.
Equate the zeros to zero:
x = 2
Subtract 2 from both sides:
x - 2 = 2 - 2
x - 2 = 0
x = (3 - 2i)
Since this root is a complex conjugate, we have the other complex root: (3 + 2i)
Hence, we have:
(x - (3 - 2i)) and (x - (3 + 2i)).
Therefore, to write the function, we have:
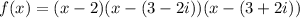
Now, simplify the expression:
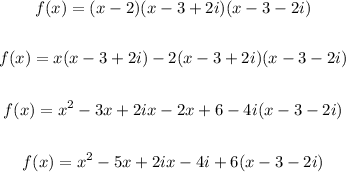
Solving further:
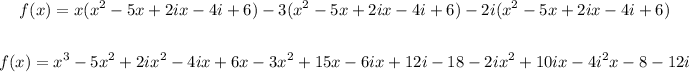
Combine like terms:
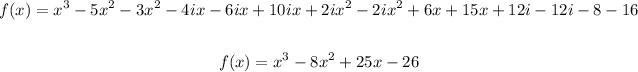
ANSWER:
