1 Answer

Gimel · Answer 1 · 2023-01-19T07:23:09+0000

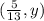
This is given point in the fourth quadrant.

In this point, the adjacent is

The opposite is y.

Find hypotenuse h using the pythagorean theorem:

$\begin{gathered} h^2=((5)/(13))^2+y^2 \\ h=\sqrt[]{(25)/(169)+y^2} \end{gathered}$
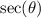
$\sec (\theta)$

is equal to hypotenuse by adjacent.

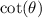
$\cot (\theta)$

is equal to adjacent by opposite.

In the fourth quadrant,

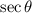
$\sec \theta$

is positive , and

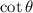
$\cot \theta$

is negative.

So,

$\begin{gathered} \sec \theta=(h)/((5)/(13)) \\ =\frac{13\sqrt[]{(25)/(169)+y^2}}{5} \\ \cot \theta=((5)/(13))/(-y) \\ =-(5)/(13y) \end{gathered}$

Please log in or register to add a comment.