Question

Find the area of the prism in the figure shown.

Answer 1

TherWe are asked to determine the area of the triangular prism. To do that we will add the area of the surfaces of the prism and add them together.

we have that the front and back areas are the areas of a triangle which is given by the following formula:

`A_t=(bh)/(2)`

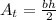
Where:

`\begin{gathered} b=\text{ length of the base} \\ h=\text{ height of the triangle} \end{gathered}`

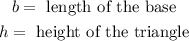
In this case, we have:

`\begin{gathered} b=3 \\ h=4 \end{gathered}`

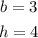
Substituting the values we get:

`A_t=(\left(3\right)\lparen4))/(2)`

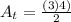
Solving the operations:

`A_t=6`

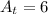
Since the front and back faces are the same triangle we can multiply the result by 2:

`A_t=2*6=12`

Therefore, the areas of the front and back faces add up to 12.

Now, we determine the area of the right side. This is the area of a rectangle and is given by the following formula:

`A_r=lh`

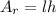
Where:

`\begin{gathered} l=\text{ length of the rectangle} \\ h=\text{ height of the rectangle} \end{gathered}`

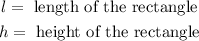
In this case, we have:

`\begin{gathered} l=5 \\ h=4 \end{gathered}`

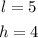
Substituting the values we get:

`A_r=\left(5\right)\left(4\right)`

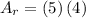
Solving the operation:

`A_r=20`

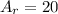
Now, we determine the area of the left face which is also a rectangle with the following dimensions:

`\begin{gathered} h=5 \\ l=5 \end{gathered}`

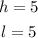
Substituting we get:

`A_l=\left(5\right)\left(5\right)=25`

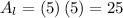
Therefore, the area of the left side is 25.

The area of the bottom face is also a rectangle with the following dimensions:

`\begin{gathered} h=5 \\ l=3 \end{gathered}`

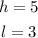
Substituting we get:

`A_b=\left(5\right)\left(3\right)=15`

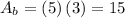
Now, the total surface area is the sum of the areas of each of the faces:

`A=A_t+A_r+A_l+A_b`

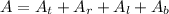
Substituting the values we get:

`A=12+20+25+15`

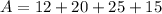
Solving the operations:

`A=72`

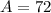
Therefore, the surface area is 72.