Question

3 3 Luke started a weight-loss program. The first week, he lost x pounds. The second week, he lost 2 pounds less than 2 times the pounds 3 he lost the first week. The third week, he lost 1 pound more than ã of the pounds he lost the first week. 3 Liam started a weight-loss program when Luke did. The first week, he lost 1 pound less than 2 times the pounds Luke lost the first 5 week. The second week, he lost 4 pounds less than 2 times the pounds Luke lost the first week. The third week, he lost 2 pound more 5 than 3 times the pounds Luke lost the first week. Assuming they both lost the same number of pounds over the three weeks, complete the following sentences. 4 pounds 6 pounds 21 4 2 pounds 13 - 40Luke started a weight loss program the first week he lost X pounds the second week he lost 3/2 pounds less than 3/2 times the pounds he lost the first week the third week he lost 1 pound more than three-fourths of the Pouncey lost the first week

Answer 1

We know that Luke lost x pounds the first week.

We also know that the second week 3/2 less than 3/2 times the pounds he lost the first week, this means that the secons week he lost:

`(3)/(2)x-(3)/(2)`

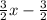
Finally the third week he lost 1 pound more than 3/4 of the pounds he lost the first week. This can be written as:

`(3)/(4)x+1`

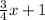
Hence luke lost a total of:

`x+(3)/(2)x-(3)/(2)+(3)/(4)x+1=(13)/(4)x-(1)/(2)`

Therefore the expression for Luke's weight loss is:

`(13)/(4)x-(1)/(2)`

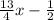
Liam lost the first week 1 pound less than 3/2 times the loss Luke had the first week this can be express as:

`(3)/(2)x-1`

The second week he lost 4 pounds less than 5/2 times the loss of Luke the firs week then we have:

`(5)/(2)x-4`

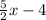
Finally Liam lost 1/2 pound more than 5/4 times the loss of Luke the first week, then:

`(5)/(4)x+(1)/(2)`

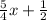
Adding this we have:

`(3)/(2)x-1+(5)/(2)x-4+(5)/(4)x+(1)/(2)=(21)/(4)x-(9)/(2)`

Therefore Liam's expression is:

`(21)/(4)x-(9)/(2)`

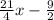
Now, we know that both of them lost the same weight, then we have the equation:

`(13)/(4)x-(1)/(2)=(21)/(4)x-(9)/(2)`

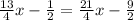
Solving for x we have:

`\begin{gathered} (13)/(4)x-(1)/(2)=(21)/(4)x-(9)/(2) \\ (21)/(4)x-(13)/(4)x=(9)/(2)-(1)/(2) \\ (8)/(4)x=4 \\ x=(4)/((8)/(4)) \\ x=2 \end{gathered}`

Therefore Luke lost 2 pound the first week.

Finally we plug the value of x in the expression for Luke's weight loss to get the total amount over the three weeks:

`\begin{gathered} (13)/(4)(2)-(1)/(2)=(13)/(2)-(1)/(2) \\ =(12)/(2) \\ =6 \end{gathered}`

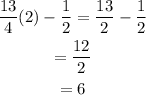
Therefore they lost 6 pounds in three weeks.