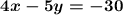We know that two lines are parallel if they have the same slope. So we first find the slope of the given line. One way to do this is to rewrite the equation in its slope-intercept form, solving for y:
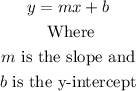
Then, we have:

Now, we have the slope and a point through which the line passes:
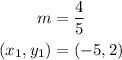
Then, we can use the point-slope formula:
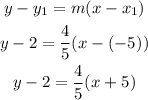
The above equation is the equation of the line in its point-slope form. However, we can also rewrite the equation of the line in its standard form by solving for the constant:
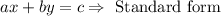

Therefore, an equation of the line that passes through the point (-5,2) and is parallel to the line 4x - 5y = 5 is