Step-by-step explanation
Firstly, let's draw a picture of the distribution:
Graphically, we want to calculate the blue area. To put it differently, we want to calculate
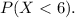
To do this, we need to find the z-score associated with 6. We can calculate it by
![\begin{gathered} z=(6-\mu)/(\sigma)\Rightarrow\begin{cases}\mu=\operatorname{mean} \\ \sigma=\text{standard deviation}\end{cases}, \\ \\ z=(6-\mu)/(\sigma)=(6-9.2)/(1.1)\approx-2.91. \end{gathered}]()
Now, we must check our favorite z-score table and look for the probability associated with the z-score we just found. It's 0.0018.
Answer
The probability that a randomly selected TV will have a warranty of less than 6 years is 0.0018.