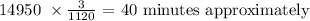Question

It takes a hose 3 minutes to fill a rectangular aquarium 8 inches long, 10 inches wide, and 14 inchestall. How long will it take the same hose to fill an aquarium measuring 23 inches by 25 inches by 26inches?minutesEnter an integer or decimal number [more..]Round your answer to the nearest minuteSubmit

Answer 1

`40\text{ minutes}`

Step-by-step explanation:

Firstly, we have to calculate the rate at which the hose works

We can get that by dividing the volume of the first aquarium by the time taken to fill it

The volume of the first aquarium can be calculated using the formula:

`V\text{ = L}* B* H`

Where:

L is the length of the aquarium

B is its width

H is its height

The volume of the first aquarium is thus:

`V\text{ = 8}*10*14\text{ = 1120 in}^3`

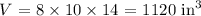
We have the filling rate as:

`(1120)/(3)\text{ in}^3\text{ per minute}`

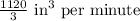
Now, let us get the volume of the second aquarium

We use the same formula as the first

We have the volume as:

`23*25*26\text{ = 14,950 in}^3`

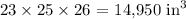
Now, to get the time taken, we divide the volume of the second aquarium by the rate of the first

Mathematically, we have that as:

`14950\text{ }*(3)/(1120)\text{ = 40 minutes approximately}`