Question

Write an equation of a line in SLOPE INTERCEPT FORM that goes through (-5,-3) and is parallel to the line y = x +5.

Answer 1

Since the slope of the line y=x+5 is m=1, then if the other line is parallel to y=x+5, then it must have the same slope, this is, m'=1.

Now we can use the point-slope formula to get the equation of the line:

`\begin{gathered} m^(\prime)=1 \\ (x_0,y_0)=(-5,-3) \\ y-y_0=m(x-x_0) \\ \Rightarrow y-(-3)=1\cdot(x-(-5))=x+5 \\ \Rightarrow y+3=x+5 \\ \Rightarrow y=x+5-3=x+2 \\ y=x+2 \end{gathered}`

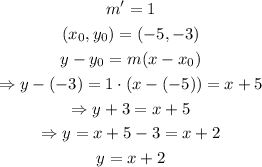
therefore, the equation of the line in slope intercept form that goes through (-5,-3) and is parallel to the line y=x+5 is y=x+2