Question

In the inequality 6a+4b>10, what could be the possible value of a if b=2?

Answer 1

We are given the following inequality:

`6a+4b>10`

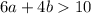
If we replace b = 2, we get:

`\begin{gathered} 6a+4(2)>10 \\ 6a+8>10 \end{gathered}`

Now we solve for "a" first by subtracting 8 on both sides:

`\begin{gathered} 6a+8-8>10-8 \\ 6a>2 \end{gathered}`

Now we divide both sides by 6

`(6a)/(6)>(2)/(6)`

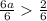
Simplifying:

`a>(1)/(3)`

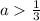
Therefore, for b = 2, the possible values of "a" are those that are greater than 1/3