Question

F(x) = x^3- 9x^2 + 10.c ) list the x values of all the inflection points of F

Answer 1

To find the inflection points the first step we have to follow is to find the second and third derivatives of the function:

`\begin{gathered} f\mleft(x\mright)=x^3-9x^2+10 \\ f^(\prime)\left(x\right)=3x^2-18x \\ f^(\prime)^(\prime)\left(x\right)=6x-18 \\ f^(\prime)^(\prime)^(\prime)\left(x\right)=6 \end{gathered}`

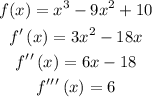
Now, find the values of x for which the second derivative is 0:

`\begin{gathered} 0=6x-18 \\ 18=6x \\ x=(18)/(6) \\ x=3 \end{gathered}`

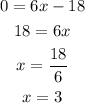
Evaluate the third derivative at this values of x, if the third derivative is different from 0, then that value is an inflection point:

`f^(\prime)^(\prime)^(\prime)\left(3\right)=6`

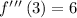
It means that there is an inflection point at x=3.