Answers:
- System 1: x = 3 and y = -5
- System 2: x = 1 and y = 2
==========================================================
Step-by-step explanation:
For now, let's focus on system 1.
We have identical copies of "2y" in each equation, which means that if we were to subtract the equations straight down, then the y terms cancel out. That allows us to solve for x.
- The x terms subtract to 7x-x = 6x
- The y terms subtract to 0 and go away
- The right hand sides subtract to 11 minus (-7) = 11-(-7) = 11+7 = 18
After doing those subtractions, we have the new equation 6x = 18 which solves to x = 3. Divide both sides by 6 to isolate x.
Once we know x, we can find out y.
7x+2y = 11
7(3)+2y = 11
21+2y = 11
2y = 11-21
2y = -10
y = -10/2
y = -5
or we can say
x+2y = -7
3+2y = -7
2y = -7-3
2y = -10
y = -10/2
y = -5
We should lead to the same y value either way. This helps confirm we have the correct x value.
Overall, the solution to system 1 is (x,y) = (3, -5)
----------------------------
Now onto system 2.
Unfortunately, we don't have identical y terms this time. But what we can do is double everything in the second equation to go from -x+y = 1 to -2x+2y = 2.
The new equivalent system is
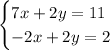
Now we have the same situation as before: Subtract straight down, solve for x.
- The x terms subtract to 7x-(-2x) = 7x+2x = 9x
- The y terms go away when subtracting
- The right hand sides subtract to 11-2 = 9
So we have 9x = 9 and that solves to x = 1.
We'll use this x to find the y value.
7x+2y = 11
7(1)+2y = 11
7+2y = 11
2y = 11-7
2y = 4
y = 4/2
y = 2
Or you could pick on the second equation
-x+y = 1
-1+y = 1
y = 1+1
y = 2