Question

xThe number of hours of daylight in a city in the Northern hemisphere shows periodic behavior over time.• The average number of daylight hours is 12.• The maximum number of daylight hours is 14.4.• The period is 365 days.• The day with the least sunlight is December 20.Which equation models the number of hours of daylight on the day that comes t days after the shortest day of the previous year?

Answer 1

Step-by-step explanation

Since we know that the number of hours is represented by a periodic function, the appropriate model is the sine function.

As the average number of daylight hours is 12 with a maximum and minimum of 14.4 and 9.6 respectively.

Furthermore, the period is 365.

Thus, the period is as follows:

`(2\pi)/(365)=0.017`

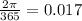
The appropiate model is the following:

`H(t)=a\sin(0.017t)+12`

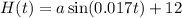
Now, we need to compute the value of a:

Since the sine function reaches its highest value at t=90° and is represented by 14.4, when t=90°, the value of the function is asin(0.017t) = 1

Therefore,

14.4 = a + 12

Subtracting -12 to both sides:

14.4 - 12 = a

Subtracting numbers:

2.4 = a

In conclusion, the final function is the following:

`H(t)=2.4\sin(0.017t)+12`

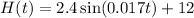
Since the minimum is at t=0, we want:

`H\left(t\right)=-2.4cos\left(0.017t\right)+12`

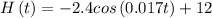
In conclusion, the solution is the OPTION C)