Question

The probability that a tourist- will spot a Cheetah in Kruger National park is 0.4, the probability that he will spot a Tiger, is 0.7, and the probability that he will spot a Cheetah, or a Tiger or both is 0.5. What is the probability that the tourist will spot: (a) both animals? (b) neither of the animals? (c) Determine with appropriate reason whether the event of spotting a Cheetah and a Tiger are independent or not?

Answer 1

Since the probability of Cheetah is 0.4

Since the probability of Tiger is 0.7

Since the probability of Cheetah or Tiger or both is 0.5

Let us draw a figure to show this information

Then we need to find both animals (x)

Since

`0.5+x=0.7+0.4-x`

Add x to both sides and subtract 0.5 from both sides

`\begin{gathered} 0.5+x+x=0.7+0.4-x+x \\ 0.5+2x=1.1 \\ 0.5-0.5+2x=1.1-0.5 \\ 2x=0.6 \end{gathered}`

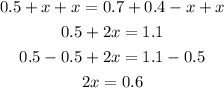
Divide both sides by 2 to find x

`\begin{gathered} (2x)/(2)=(0.6)/(2) \\ x=0.3 \end{gathered}`

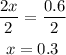
a) The probability of both animals is 0.3

Since the total of probability is 1, then to find the neither subtract (0.4 + 0.7 - 0.3) from 1

`\begin{gathered} N=1-(0.4+0.7-0.3) \\ N=1-0.8 \\ N=0.2 \end{gathered}`

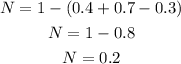
b) the probability of neither is 0.2

Events A and B are independent if the equation P(A∩B) = P(A) · P(B)

Since

`P(Ch\cap T)=0.3`

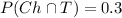
Since P(Ch) . P(T) = 0.4 x 0.7 = 0.28

Then

`P(Ch\cap T)\\e P(Ch).P(T)`

c) The events are not independent