A pair of numbers that have a sum of 50
Let the number is x, so the other number is 50 - x
Let f(x) be the largest product so:
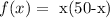
Simplify the expression :

Diffrentiate with respect to x
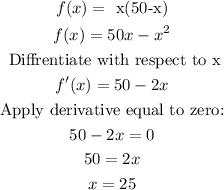
Now for to check for the f(x) is maximum for x = 25
Calculate the second derivative and put x = 25 is the f(x) is negative then the multiplication f(x) is maximum

Thus, the first number is 25
Second number is : 50 -x = 50-25 = 25
Numbers are 25, 25
Answer : 25 + 25 =50 (sum)
25 * 25 = 625 (maximum possible product)