Question

Suppose the commute times for employees of a large company follow anormal distribution. If the mean time is 24 minutes and the standarddeviation is 5 minutes, 95% of the employees will have a travel time within which range?

Answer 1

The empirical rule state that, for normally distributed data, almost all of the data fall within three standard deviations either side of the mean. Specifically,

-68% of data within 1 standard deviation.

-95% of data within 2 standard deviation

-99.7 of data within 3 standard deviation.

In our case the mean is

`\mu=24`

and the standard deviation is

`\sigma=5`

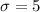
then, the empirical formula imply that

`\begin{gathered} \mu-2\sigma=24-2\cdot5 \\ \mu-2\sigma=24-10 \\ \mu-2\sigma=14 \end{gathered}`

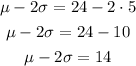
and

`\begin{gathered} \mu+2\sigma=24+2\cdot10 \\ \mu+2\sigma=24+10 \\ \mu+2\sigma=34 \end{gathered}`

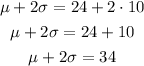
then, the answer is 14 minutes to 34 minutes