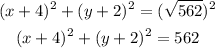In this problem, we are going to find the formula for a circle from the center and a point on the circle. Let's begin by reviewing the standard form of a circle:

The values of h and k give us the center of the circle, (h,k). The value r is the radius. We can begin by substituting the values of h and k into our formula.
Since the center is at (-4, -2), we have:
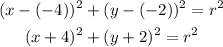
Next, we can use the center and the given point on the circle to find the radius.
Recall that the radius is the distance from the center of a circle to a point on that circle. So, we can use the distance formula:
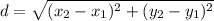
Let
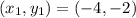
and let
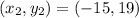
Now we can substitute those values into the distance formula and simplify.

Adding that to our equation, we have: