In the given figure, m∠2 and m∠7 are "Alternate Exterior Angles" and they are always congruent (equal).
So we can equate them and solve for x.
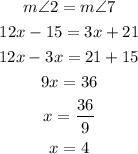
So, m∠2 is
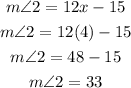
According to the straight-line angle property, the sum of m∠1 and m∠2 must be equal to 180°
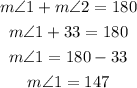
Therefore, the measure of m∠1 is 147°