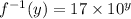Part b.
In this case, we have the following function:
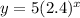
First, we need to solve for x. Then, by applying natural logarithm to both sides, we have
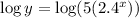
By the properties of the logarithm, it yields
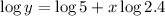
By moving log5 to the left hand side, we have
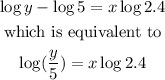
By moving log2.4 to the left hand side, we obtain
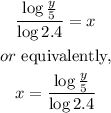
Therfore, the answer is
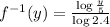
Part C.
In this case, the given function is
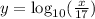
and we need to solve x. Then, by raising both side to the power 10, we have
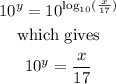
By moving 17 to the left hand side, we get
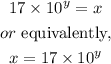
Therefore, the answer is