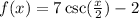Question

I need help with this practice problem I’m having trouble solving it

Answer 1

A generic cosecant function is

`f(x)=A\csc (kx+\theta)+C`

We must find A, k, θ, and C using the information that we have.

Finding A:

To find A we can use the range of the function, we know there is a gap between -9 and 5, that's the crucial information, the value of A will be the mean of |-9| and |5| (in modulus!), therefore

`A=(|-9|+|5|)/(2)=(9+5)/(2)=(14)/(2)=7`

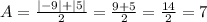
Therefore

`f(x)=7\csc (kx+\theta)+C`

Finding C:

We can use the fact that we know A and find C, let's suppose that

`\csc (kx+\theta)=1`

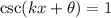
For an unknown value of x, it doesn't matter, using the range again we can use the fact that 5 is a local minimum of the function, therefore, when the csc(kx + θ) is equal to 1 we have that the function is equal to 5

`\begin{gathered} 5=7\cdot1+C \\ \\ C=-2 \end{gathered}`

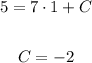
And we find that C = -2. Tip: You can also suppose that it's -1 and use -9 = 7 + C, the result will be the same.

Finding k:

Now we will use the asymptotes, we have two consecutive asymptotes at x = 0 and x = 2π, it means that the sin(kx) is zero at x = 0 and the next zero is at x = 2π, we know that sin(x) is zero every time it's a multiple of π, which gives us

`\begin{gathered} \sin (0)=0\Rightarrow\sin (k\cdot0)=0\text (first zero \\ \sin (\pi)=0\Rightarrow\sin (2k\pi)=0\Rightarrow k=(1)/(2)\text (second zero \end{gathered}`

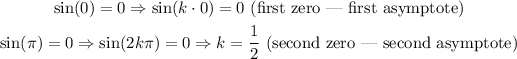
Therefore, k = 1/2

`f(x)=7\csc ((x)/(2)+\theta)-2`

Finding θ:

It's the easiest one, since we have a zero at x = 0 it implies that θ = 0

Therefore our function is

`f(x)=7\csc ((x)/(2))-2`

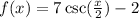
Final answer:

`f(x)=7\csc \mleft((x)/(2)\mright)-2`