We have a right triangle XYZ.
The length of the hypotenuse is YZ=85.
We also know that the tangent of Z is 4.
We have to find the length of XY.
We can start by drawing the triangle and writing the data:
The tangent of an angle can be related with the sides by the following trigonometric ratio:
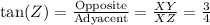
We can not find the value of the legs from the trigonometric ratio, but we have a proportion between them. We can write the previous result as:
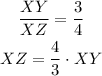
Now we can relate XY with the hypotenuse YZ using the Pythagorean theorem:
![\begin{gathered} XY^2+XZ^2=YZ^2 \\ XY^2+((4)/(3)XY)^2=YZ^2 \\ XY^2+(16)/(9)XY^2=YZ^2 \\ ((16)/(9)+1)XY^2=YZ^2 \\ (16+9)/(9)XY^2=YZ^2 \\ (25)/(9)XY^2=YZ^2 \\ XY^2=(9)/(25)YZ^2 \\ XY=\sqrt[]{(9)/(25)YZ^2} \\ XY=(3)/(5)YZ \\ XY=(3)/(5)\cdot85 \\ XY=51 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/1dg9k08ghnco8f374iononky1nlecsx5hh.png)
Answer: the length of the leg XY is 51 inches.