Given a quadratic equation of the form:

The discriminant is:
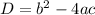
And we can know the number of solutions with the value of the discriminant:
• If D < 0, the equation has 2 imaginary solutions.
,
• If D = 0, the equation has 1 real solution
,
• If D > 0, the equation has 2 real solutions.
Equation One:
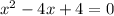
Then, we calculate the discriminant:
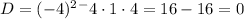
D = 0
There are 1 real solution.
Equation Two:
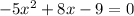
Calculate the discriminant:
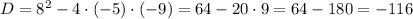
D = -116
There are 2 imaginary solutions.
Equation Three:
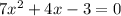
Calculate the discriminant:
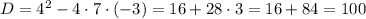
D = 100
There are 2 real solutions.
Answers:
Equation 1: D = 0, One real solution.
Equation 2: D = -116, Two imaginary solutions.
Equation 3: D = 100, Two real solutions.