Question

Can someone help me with this geometry question? I will provide more information.

Answer 1

So you are given a triangle ABC and you need to build another one DEF that meets the following:

`\begin{gathered} AB=DE \\ m\angle E=90^(\circ) \\ EF=BC \end{gathered}`

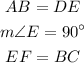
First of all we should find the lengths of sides AB and BC. For this purpose we can use the coordinates of points A, B and C. The length of AB is the distance between A and B and the length of BC is the distance between B and C. The distance between two generic points (a,b) and (c,d) is given by:

`\sqrt[]{(a-c)^2+(b-d)^2}`

Then the length of AB is:

`AB=\sqrt[]{(1-1)^2+(6-1)^2}=\sqrt[]{0+5^2}=5`

And that of BC is:

`BC=\sqrt[]{(1-5)^2+(1-1)^2}=\sqrt[]{4^2}=4`

Then the triangle DEF must meet these three conditions:

`\begin{gathered} DE=5 \\ EF=4 \\ m\angle E=90^(\circ) \end{gathered}`

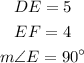
Since there is no rules about its position we can draw it anywhere. For example you can choose E=(-4,1). Then if D=(-4,6) we have that the length of DE is 5:

`DE=\sqrt[]{(-4-(-4))^2+(6-1)^2}=\sqrt[]{0+5^2}=5`

And if we take F=(0,1) we get EF=4:

`EF=\sqrt[]{(-4-0)^2+(1-1)^2}=\sqrt[]{16}=4`

Then a possibility for triangle DEF is:

As you can see it also meets the condition that the measure of E is 90°. And that would be part A.

In part B we have to use the pythagorean theorem to state a relation between the sides of DEF. For a right triangle with legs a and b the theorem states that its hypotenuse h is given by:

`h^2=a^2+b^2`

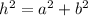
We can do the same for DEF. Its legs are DE and EF whereas its hypotenuse is DF so we get:

`DF^2=DE^2+EF^2`

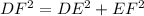
And that's the equation requested in part B.