Given the quadratic equation:
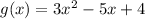
Let's solve for the following:
• (a) g(-3)
To solve for g(-3), substitute -3 for x and evaluate.
Thus, we have:
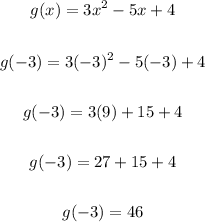
Hence, we have:
g(-3) = 46
• (b) To determine the coordinates of the point given in question (a).
In the function, g(x) can also be written as y.
Thus, from g(-3), we have the following:
x = -3
y = 46
When x = -3, the value of y = 46
In point form, we have the coordinates:
(x, y) ==> (-3, 46)
Therefore, the coordinates of the given point by the answer in (a) is:
(-3, 46)
• (c) Evaluate g(2a).
To evaluate g(2a), substitute 2a for x in the equation and evaluate.
Thus, we have:
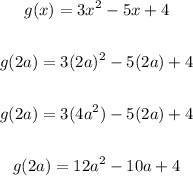
ANSWERS:
• (a) g(-3) = 46
• (b) (-3, 46)
• (c) g(2a) = 12a² - 10a + 4