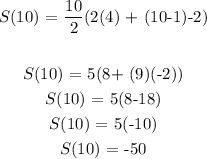Answer:
Step-by-step explanation:
Here, we want to work with an arithmetic series
a) First term
The first term (a) of the arithmetic is the first number on the left
From the question, we can see that this is 4
Hence, 4 is the first term
To find the common difference, we have this as the difference between twwo subsequent terms, going from left to right
We have this as:
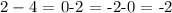
The common difference d is -2
ii) We want to calculate the sum of the first 10 terms
The formula for this is:
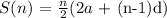
Where S(n) is the sum of n terms
n is the number of terms which is 10
a is the first term of the series which is 4
d is the common difference which is -2
Substituting these values, we have it that: