Question

Question 7, pre calc, include the answer in bold please. I have bad WiFi so please finish question if I get disconnected so I can see it, thanks

Answer 1

Given the following function

`f(x)=x^4-x^3+7x^2-9x-18`

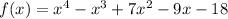
We want to find its roots. Since we already know that (x + 1) and (x - 2) are factors of this polynomial, we can divide our polynomial by those factors and factorize the result to get the other roots.

Let's start by dividing by the first factor

`(x^4-x^3+7x^2-9x-18)/(x+1)`

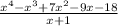
To divide a polynomial by other, we start by dividing the leading term of the dividend by the leading term of the divisor(this will be the first term of our result)

`(x^4)/(x)=x^3`

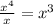
Then, we ultiply it by the divisor

`x^3(x+1)=x^4+x^3`

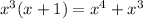
Subtracting this result from the dividend, we have

`(x^4-x^3+7x^2-9x-18)-(x^4+x^3)=-2x^3+7x^2-9x-18`

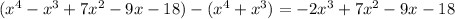
This means that our division is

`(x^4-x^3+7x^2-9x-18)/(x+1)=x^3+(-2x^3+7x^2-9x-18)/(x+1)`

Repeating the whole process of division with the second term, we have

`\begin{gathered} x^3+(-2x^3+7x^2-9x-18)/(x+1)=x^3-2x^2+(9x^2-9x-18)/(x+1) \\ \Rightarrow(x^4-x^3+7x^2-9x-18)/(x+1)=x^3-2x^2+9x-18 \end{gathered}`

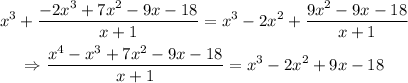
From this result, we can rewrite our function as

`x^4-x^3+7x^2-9x-18=(x+1)(x^3-2x^2+9x-18)`

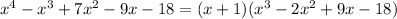
Repeating this same process with the other know factor, the other division we have to solve is

`((x^3-2x^2+9x-18))/(x-2)=x^2+9`

Then, our function is

`f(x)=(x^4-x^3+7x^2-9x-18)=(x+1)(x-2)(x^2+9)`

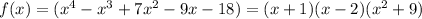
Then, to find the roots we need to solve the following equation

`(x+1)(x-2)(x^2+9)=0`

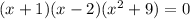
Since we have a product of 3 terms, the result will be zero if and only if one of the terms is zero. This means that the roots can be found by assuming each one is zero. The solutions for this equation are the same solutions for the following system

`\begin{cases}x+1=0 \\ x-2=0 \\ x^2+9=0\end{cases}\Rightarrow\begin{cases}x=-1 \\ x=2 \\ x=\pm\sqrt[]{-9}=\pm3i\end{cases}`

And those are the roots for our function. x = -1, 2, +-3i.