Question

The length of a rectangular pool is 6 meters less than twice the width. If the pools perimeter is 84 meters, what is the width? A) Write Equation to model the problem (Use X to represent the width of the pool) B) Solve the equation to find the width of the pool (include the units)

Answer 1

I have a problem with the perimeter of a pool expressed in an unknown which corresponds to "x"

The first thing to do is to pose the corresponding equation, this corresponds to section A of the question

For the length, we have a representation of twice the width minus 6, i.e. 2x-6

For the width we simply have x

Remember that the sum of all the sides is equal to the perimeter which is 84, However, we must remember that in a rectangle we have 4 sides where there are two pairs of parallel sides, so we must multiply the length and width by 2

Now we can represent this as an equation

`2(2x-6)+2x=84`

This is the answer A

Now let's solve the equation for part B.

`\begin{gathered} 2(2x-6)+2x=84 \\ 4x-12+2x=84 \\ 6x=84+12 \\ x=(96)/(6) \end{gathered}`
`x=16`

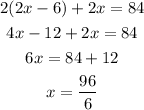
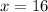
In conclusion, the width of the pool is 16