Question

Cynthia wants to buy a rug for a room that is 18ft wide and 28ft long. She wants to leave a uniform strip of floor around the rug. She can afford to buy 264 square feet of carpeting. What dimensions should the rug have ?

Answer 1

Let us use a diagram to illustrate the information, we have

Now, from the diagram, let the length of the uniform strip of floor around the rug be x, So, this means the length and width of the rug is

`\begin{gathered} \text{length = 2}8-x-x=28-2x \\ \text{width = }18-x-x=18-2x \end{gathered}`

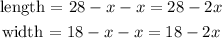
Now, since she can afford to buy a rug of 264 square feet for carpeting, this means that the area of the rug is 264, hence we have that

`\begin{gathered} \text{area of rug = (2}8-2x)*(18-2x) \\ 264=\text{(2}8-2x)(18-2x) \\ \text{(2}8-2x)(18-2x)=264 \end{gathered}`

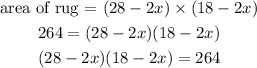
Solving for x, we have

`\begin{gathered} \text{(2}8-2x)(18-2x)=264 \\ 504-56x-36x+4x^2=264 \\ 504-92x+4x^2=264 \\ 4x^2-92x+504-264=0 \\ 4x^2-92x+240=0 \end{gathered}`

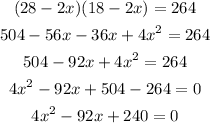
Dividing through by 4 we have

`\begin{gathered} x^2-23x+60=0 \\ x^2-20x-3x+60=0 \\ x(x-20)-3(x-20)=0 \\ (x-3)(x-20)=0 \\ x=3\text{ or 20} \end{gathered}`

So from our calculation, we go for x = 3, because 20 is large look at this

`\begin{gathered} \text{From the length which is (2}8-2x) \\ 28-2(20) \\ =28-40=-12 \end{gathered}`

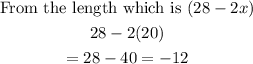
length cannot be negative, so we go for x = 3.

Hence the dimensions of the rug becomes

`\begin{gathered} \text{(2}8-2x) \\ =28-2(3) \\ =28-6=22 \\ \text{and } \\ 18-2x \\ 18-2(3) \\ 18-6=12 \end{gathered}`

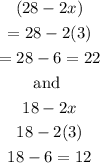
So the dimension of the rug should be 22 x 12 feet