Question

Find the coordinates of the circumcenter of triangle PQR with vertices P(-2,5) Q(4,1) and R(-2,-3)

Answer 1

The given triangle has vertices at:

`\begin{gathered} P(-2,5) \\ Q(4,1) \\ R(-2,-3) \end{gathered}`

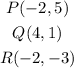
In the coordinate plane, the triangle looks like this:

There are different forms to find the circumcenter, we are going to use the midpoint formula:

`M(x,y)=((x1+x2)/(2),(y1+y2)/(2))`

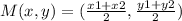
Apply this formula for each vertice and find the midpoint:

`M_(P,Q)=((-2+4)/(2),(5+1)/(2))=(1,3)`

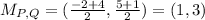
For QR:

`M_(Q,R)=((4+(-2))/(2),(1+(-3))/(2))=(1,-1)`

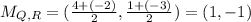
For PR:

`M_(P,R)=((-2+(-2))/(2),(5+(-3))/(2))=(-2,1)`

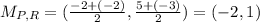
Now, we need to find the slope for any of the line segments, for example, PQ:

We can apply the slope formula:

`m=(y2-y1)/(x2-x1)=(1-5)/(4-(-2))=(-4)/(6)=-(2)/(3)`

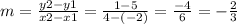
By using the midpoint and the slope of the perpendicular line, find out the equation of the perpendicular bisector line, The slope of the perpendicular line is given by the formula:

`\begin{gathered} m1\cdot m2=-1 \\ m2=-(1)/(m1) \\ m2=-(1)/(-(2)/(3))=(3)/(2)_{} \end{gathered}`

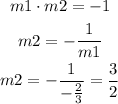
The slope-intercept form of the equation is y=mx+b. Replace the slope of the perpendicular bisector and the coordinates of the midpoint to find b:

`\begin{gathered} 3=(3)/(2)\cdot1+b \\ 3-(3)/(2)=b \\ b=(3\cdot2-1\cdot3)/(2)=(6-3)/(2) \\ b=(3)/(2) \end{gathered}`

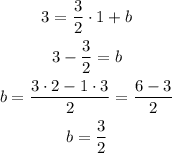
Thus, the equation of the perpendicular bisector of PQ is:

`y=(3)/(2)x+(3)/(2)`

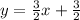
If we graph this bisector over the triangle we obtain:

Now, let's find the slope of the line segment QR:

`m=(-3-1)/(-2-4)=(-4)/(-6)=(2)/(3)`

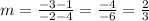
The slope of the perpendicular bisector is:

`m2=-(1)/(m1)=-(1)/((2)/(3))=-(3)/(2)`

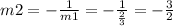
Let's find the slope-intercept equation of this bisector:

`\begin{gathered} -1=-(3)/(2)\cdot1+b \\ -1+(3)/(2)=b \\ b=(-1\cdot2+1\cdot3)/(2)=(-2+3)/(2) \\ b=(1)/(2) \end{gathered}`

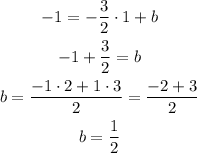
Thus, the equation is:

`y=-(3)/(2)x+(1)/(2)`

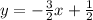
This bisector in the graph looks like this:

Now, to find the circumcenter we have to equal both equations, and solve for x:

`\begin{gathered} (3)/(2)x+(3)/(2)=-(3)/(2)x+(1)/(2) \\ \text{Add 3/2x to both sides} \\ (3)/(2)x+(3)/(2)+(3)/(2)x=-(3)/(2)x+(1)/(2)+(3)/(2)x \\ (6)/(2)x+(3)/(2)=(1)/(2) \\ \text{Subtract 3/2 from both sides} \\ (6)/(2)x+(3)/(2)-(3)/(2)=(1)/(2)-(3)/(2) \\ (6)/(2)x=-(2)/(2) \\ 3x=-1 \\ x=-(1)/(3) \end{gathered}`

Now replace x in one of the equations and solve for y:

`\begin{gathered} y=-(3)/(2)\cdot(-(1)/(3))+(1)/(2) \\ y=(1)/(2)+(1)/(2) \\ y=1 \end{gathered}`

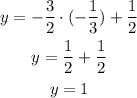
The coordinates of the circumcenter are: (-1/3,1).

In the graph it is: