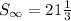Answer:
The sum to infinity of the given series is;
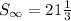
Step-by-step explanation:
From the given series, we can see that the series is a Geometric Progression (GP) because it has a common ratio;
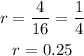
The formula to calculate the sum to infinity of a GP is;
![\begin{gathered} S_(\infty)=(a)/(1-r) \\ \text{For;} \\ 0Where;<p>a = first term = 16</p><p>r = common ratio = 0.25.</p><p></p><p>substituting we have;</p>[tex]\begin{gathered} S_(\infty)=(16)/(1-0.25)=(16)/(0.75) \\ S_(\infty)=21(1)/(3) \\ S_(\infty)=21.33 \end{gathered}]()
Therefore, the sum to infinity of the given series is;