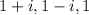We know that 1+i is a root of the polynimial. This also implies that 1-i is also a root of the polynomial. In other words, the term
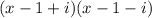
is a factor of our polynomial. This last expression can be written as

so, in order to find the remaining zero, we can compute the following division of polynomials,
which gives
Therefore, the remaining root is x=1.
In summary, the answer is: