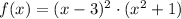Question

Find a polynomial f(x) of degree 4 with real coefficients and the following zeros.3 (multiplicity 2) , -i

Answer 1

We are told that we want a polynomial f(x) with the given zeros.

Recall that if we know the zeros oa polynomial, we can write the polynomial by writing the factors (x - zero of the polynomial) and multiply them all together.

For example, if we want a polynomial of degree 2 with zeros at 2 and 3, then the polynomial would be

`(x\text{ -2)}\cdot(x\text{ -3)}`

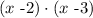
In this case, we have a polynomial f(x) of degree 4. So far, we know that 3 is a zero and that -i is a zero. So we write the following

`f(x)=(x\text{ -a)}\cdot(x\text{ -b)}\cdot(x\text{ -c) }\cdot\text{ (x -d)}`

where a,b,c and d are the zeros of f(x). We know that 3 is a zero and that -i is a zero. So we have

`f(x)=(x\text{ -3)}\cdot(x\text{ -b)}\cdot(x\text{ -( -i)) }\cdot(x\text{ -d)}`

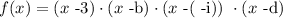
So to fully describe f(x) we need to find the values of b and d. We are told that 3 is a zero of multiplicity 2. This means that the factor (x -3) appears two times in the factorization of f(x). So we can say that b=3. So we have

`f(x)=(x\text{ -3)}\cdot(x\text{ -3) }\cdot(x\text{ +i ) }\cdot(x-d)=(x-3)^2\cdot(x\text{ +i)}\cdot(x\text{ -d)}`

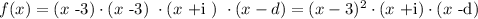
Now, we need to find the value of d. Note that we are told that -i is a zero of the function. -i is a complex number, so one important property of polynomials is that if a complex number a+bi is a zero of the polynomial, then the number a-bi (which is called the complex conjugate) is also a zero. Note that the complex conjugate of a complex number is calculated by leaving the real part intact and multiplying the imaginary part by -1.

In our case we have the complex number -i. So we can write -i= 0 - 1i . Then, its complex conjugate is i.

So, we have that d=i.

Then our polynomial would look like this

`f(x)=(x-3)^2\cdot(x+i)\cdot(x\text{ -i)}`

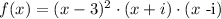
Note that

`(x+i)\cdot(x-i)=x^2\text{ -i}\cdot x\text{ + i}\cdot x+1=x^2+1`

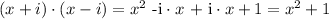
So our polynomial ends up being

`f(x)=(x-3)^2\cdot(x^2+1)`