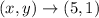Question

What is the solution to the following system of equations. Enter your answer as an ordered pair.3x+2y=17and4x+6y=26As an ordered pairHelp me pls

Answer 1

The system of equation are:

`\begin{gathered} 3x+2y=17 \\ 4x+6y=26 \end{gathered}`

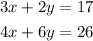
to solve this problem we can solve the second equation for x so:

`\begin{gathered} 4x=26-6y \\ x=6.5-1.5y \end{gathered}`

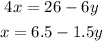
Now we can replace x in the firt equation so:

`3(6.5-1.5y)+2y=17`

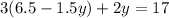
and we can solve for y so:

`\begin{gathered} 19.5-4.5y+2y=17 \\ 19.5-17=2.5y \\ 2.5=2.5y \\ (2.5)/(2.5)=1=y \end{gathered}`

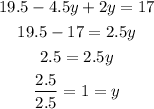
Now we replace the value of y in the secon equation so:

`\begin{gathered} x=6.5-1.5(1) \\ x=5 \end{gathered}`

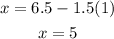
So the solution as a ordered pair is:

`(x,y)\to(5,1)`