The formula to find the area of a rectangle is:

Since the rectangle area is 170cm², we can write the following equation.

On the other hand, we know that the width of the rectangle is 6 less than twice its length. Then, we can write another equation.
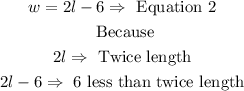
Now, we solve the found system of equations.
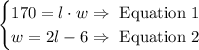
For this, we can use the substitution method.
Step 1: we replace the value of w from Equation 2 into Equation 1. Then, we solve for l.

We can use the quadratic formula to solve the above equation.
![\begin{gathered} x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}\Rightarrow\text{ Quadratic formula} \\ \text{ For }ax^2+bx+c=0 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/n7bb6wcfbmyhboqf5yp9yb626hfh9xk4j5.png)
Then, we have:
![\begin{gathered} a=2 \\ b=-6 \\ c=-170 \\ l=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ l=\frac{-(-6)\pm\sqrt[]{(-6)^2-4(2)(-170)}}{2(2)} \\ l=\frac{6\pm\sqrt[]{1396}}{4} \\ \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/xse70zun59d4ko0kcac9rl9zo7j3wao1ic.png)
There are two solutions for l.
![\begin{gathered} l_1=\frac{6+\sqrt[]{1396}}{4}\approx10.84 \\ l_2=\frac{6-\sqrt[]{1396}}{4}\approx-7.84 \\ \text{ The symbol }\approx\text{ is read 'approximately'.} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/tqq2nhskm1v2zrrytvons5fpiyi7bbfp0p.png)
Since the value of l can not be negative, the value of l is 10.84.
Step 2: We replace the value of l into any of the equations of the system to find the value of w. For example, in Equation 1.
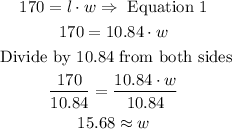
Now, the long side, the wide side and the diagonal of the rectangle form a right triangle.
Then, we can use the Pythagorean theorem formula to find the length of the diagonal.

In this case, we have:
![\begin{gathered} a=10.84 \\ b=15.68 \\ a^2+b^2=c^2 \\ (10.84)^2+(15.68)^2=c^2 \\ 117.51+245.86=c^2 \\ 363.37=c^2 \\ \text{ Apply square root to both sides of the equation} \\ \sqrt[]{363.37}=\sqrt[]{c^2} \\ 19.06=c \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/1v7j5a9anta6x9s94caduca31bbnu9ntv3.png)
Therefore, the length of the diagonal of the given rectangle is 19.06 cm rounded to 2 decimal places.