Part 1.
Since we have the equation
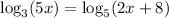
the equations which can be used to approximate the solutions are:
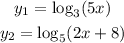
Part 2.
Let's make the graph of the 2 equations. The graph is
The approximate solution is given by the intersection point of the 2 graphs, which is the point ( 0.957 , 1.425). Then x-value corresponding to the solution is x= 0.957.