The Solution:
The listing price of the Skis by a manufacturer is $850.
A trade discount of 35% was allowed.
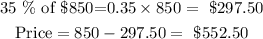
Allowing an extra discount of 18%, we get
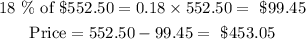
We are required to find what further rate of discount should be given to bring the net price to $446.00
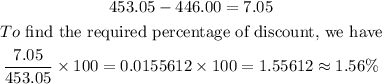
Therefore, the correct answer is 1.56%