Question

Jimmy launches his rocket straight up with an initial velocity of 25 m/s.a. What is the velocity as the rocket reaches maximum height?b. How long will it take the rocket to reach its maximum height?

Answer 1

Given that the initial velocity is u = 25 m/s.

We have to find the final velocity and time at its maximum height.

First, we need to find the maximum height.

`h\text{ =}(u)/(2g)`

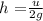
Here, g = 9.81 m/s^2 is the acceleration due to gravity.

Substituting the values, the height will be

`\begin{gathered} h=\text{ }(25)/(2*9.81) \\ =1.274\text{ m} \end{gathered}`

(a) Let the final velocity be v.

The formula to calculate final velocity is

`\begin{gathered} v^2=u^2-2gh^{} \\ v=\sqrt[]{u^2-2gh^{}} \end{gathered}`

Substituting the values, the final velocity will be

`\begin{gathered} v=\sqrt[]{\lbrack(25)^2-(2*9.81*1.274)\rbrack} \\ =\sqrt[]{600.01} \\ =24.49\text{ m/s} \end{gathered}`

(b) The time taken can be calculated by the formula,

`\begin{gathered} t=(v-u)/(-g) \\ =(24.49-25)/(-9.81) \\ =0.051\text{ s} \end{gathered}`

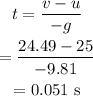
Thus, the final velocity is 24.49 m/s and time is 0.051 s