Answer:
The width of the TV is 41.84-in
Explanations:
The diagonal size of the TV, d= 48 in
The aspect ratio= 16 : 9
The aspect ratio is usually given in form of width : Height
Let the width = w
Let the height = h
The diagram looks like:
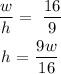
Using the Pythagoras theorem:
![\begin{gathered} d^2=h^2+w^2 \\ 48^2\text{ = (}(9w)/(16))^2+w^2 \\ 2304\text{ = }(81w^2)/(256)+w^2 \\ \text{Multiply through by 256} \\ 589824=81w^2+256w^2 \\ 589824\text{ = }337w^2 \\ w^2\text{ = }(589824)/(337) \\ w^2\text{ = 1750.22} \\ w\text{ = }\sqrt[]{1750.22} \\ w\text{ = 41.84 } \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/2uqf895xqxyk83yiquskewandnv1xdp306.png)
The width of the TV is 41.84-in