Question

Which ordered pair is in the solution set fit the system of inequalities shown below?2x-y<3x+2y>-1A. (-2,-1)B. (0,1)C. (1,-2)D.(6,1)

Answer 1

Given the System of Inequalities:

`\begin{cases}2x-y<3 \\ x+2y>-1\end{cases}`

1. Take the first inequality and solve for "y":

`\begin{gathered} -y<2x+3 \\ (-1)(-y)<(-2x+3)(-1) \\ y>2x-3 \\ \end{gathered}`

Notice that direction of the symbol changes, because you had to multiply both sides of the inequality by a negative number.

Now you can identify that the boundary line is:

`y=2x-3`

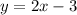
Since it is written in Slope-Intercept Form, you can identify that its slope is:

`m_1=2`

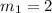
And its y-intercept is:

`b_1=-3`

Notice that the symbol of the inequality is:

`>`

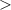
That indicates that the line is dashed and the shaded region is above the line.

Knowing all this information, you can graph the first inequality on the Coordinate Plane.

2. Apply the same procedure to graph the second inequality. Solving for "y", you get:

`\begin{gathered} 2y>-x-1 \\ \\ y>-(1)/(2)x-(1)/(2) \end{gathered}`

Notice that the boundary line is:

`y=-(1)/(2)x-(1)/(2)`

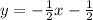
Where:

`\begin{gathered} m_2=-(1)/(2) \\ \\ b_2=-(1)/(2) \end{gathered}`

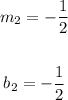
Since the symbol is:

`>`

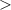
The line is dashed and the shaded region is above the line.

Knowing this, you can graph the second inequality.

3. Look at the graph of the System of Inequalities:

Notice that:

-The black line is the boundary line of the first inequality and the green line is the boundary line of the second inequality.

- The solution of the system is the intersection region. It is the region where the shaded region of the first inequality and the shaded region of the second inequality, intersect.

4. Plot the points given in the options on the graph of the Systems:

5. You can identify that this point is in the intersection region:

`(0,1)`

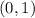
Therefore, it is a solution.

Hence, the answer is: Option B.