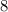Question

Given parallelogram ABCD, diagonals AC and BD intersect at point E. AE=2x, BE=y+10, CE=x+2 and DE=4y−8. Find the length of AC.A. 8B. 6C. 2D. 4

Answer 1

the length of the diagonal AC is;

`8`

Step-by-step explanation:

Given the parallelogram ABCD, diagonals AC and BD intersect at point E.

`\begin{gathered} AE=2x \\ CE=x+2 \\ BE=y+10 \\ DE=4y+8 \end{gathered}`

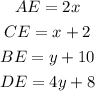
Recall that the diagonals of a parallelogram bisect each other;

So;

`AE=CE`

substituting AE and CE;

`\begin{gathered} 2x=x+2 \\ 2x-x=2 \\ x=2 \end{gathered}`

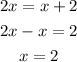
To calculate the length of AC;

`\begin{gathered} AC=2x+x+2=3x+2 \\ since\text{ x=2} \\ AC=3x+2=3(2)+2 \\ AC=6+2 \\ AC=8 \end{gathered}`

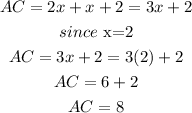
Therefore, the length of the diagonal AC is;

`8`